백준 온라인 저지, 특정 거리의 도시 찾기
TL;DR
- 다익스트라 알고리즘(Dijkstra Algorithm)
- 너비 우선 탐색(BFS)
문제 요약
1. 1번부터 N번까지 N개의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
2. 특정 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하라.
3. 최단 거리가 K인 도시를 오름차순으로 출력한다. 존재하지 않는다면 -1을 출력한다.
- 1 : N개의 노드와 M개의 간선, 간선의 가중치는 1인 그래프로 생각할 수 있다.
- 다익스트라 알고리즘을 사용하여 X 노드로부터 다른 노드들까지의 최단 경로를 확인한 뒤, 경로가 K인 노드들을 반환하면 될 것 같다.
입출력 형태
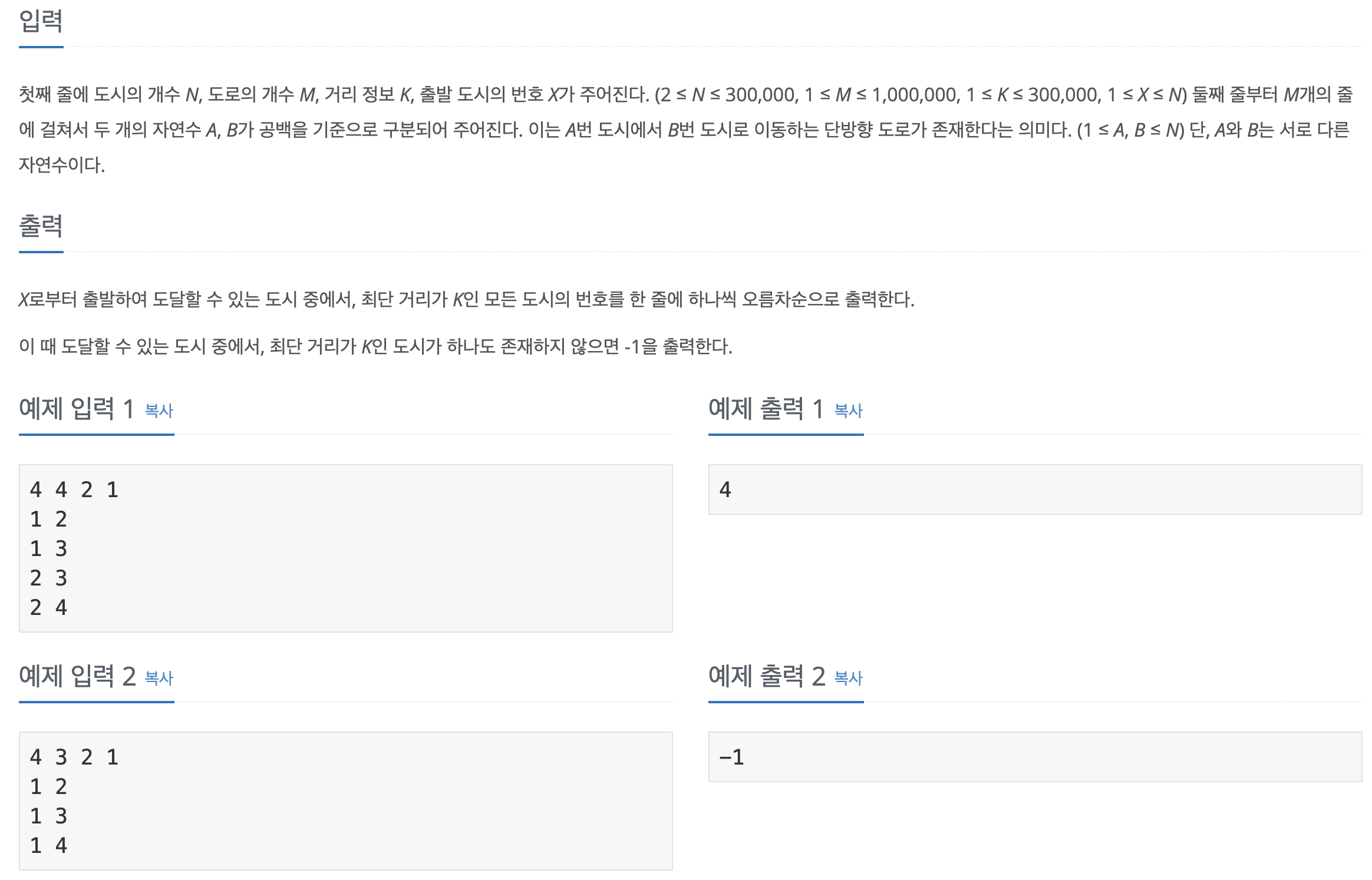
- 첫째 줄에 노드의 개수, 간선의 개수, 원하는 경로와 출발 노드의 정보가 주어진다.
- 둘째 줄부터는 각 노드의 연결 관계가 표현된다.
- 입력된 정보를 토대로 그래프를 구성하고, 그래프에서 다익스트라 알고리즘을 사용하면 된다.
풀이
import sys, collections, heapq
n, m, k, x = map(int, sys.stdin.readline().split())
answer = []
graph = collections.defaultdict(list)
for _ in range(m):
a, b = map(int, sys.stdin.readline().split())
graph[a].append((1, b))
Q = [(0, x)]
dists = collections.defaultdict(int)
while Q:
distance, vertex = heapq.heappop(Q)
if vertex not in dists:
dists[vertex] = distance
if distance == k: # 거리가 k일 경우 정답 배열에 추가
answer.append(vertex)
for w, v in graph[vertex]:
heapq.heappush(Q, (distance + w, v))
if len(answer) != 0:
print(' '.join(list(map(str, sorted(answer))))) # 오름차순 정렬 출력
else: # 경로가 존재하지 않는 경우
print('-1')
필요한 정보들을 입력받고 그래프를 딕셔너리 형태로 구성하였다. 이 딕셔너리의 key는 노드이고 value는 노드와 인접한 노드들이다.
Q는 heapq를 사용하기 위해서, dists는 각 노드까지의 최단 거리를 저장하기 위해서 선언하였다.
heapq를 사용하여 다익스트라 알고리즘을 구현하였다.
- 만약 vertex(노드)가 dists에 존재하지 않는다면 해당 vertex까지 도달하는 거리를 업데이트 한다.
- 이 때, 거리가 k와 같다면 해당 vertex를 정답 리스트에 추가한다.
- 방문한 vertex와 인접한 vertex들을 heapq에 삽입한다. 이 때, 거리를 업데이트해준다. w라고 되어 있지만 모든 가중치가 1이기 때문에 사실상 1이 추가되는 구조이다.
이 연산이 끝나고 나면 dists에는 X 노드로부터 다른 노드들까지 걸리는 최단 경로가 저장되게 되고, answer에는 최단 경로의 길이가 k인 노드들이 저장되게 된다.
- 만약, answer가 비어있지 않다면 answer 내에 있는 노드들은 k 내에 도달할 수 있는 노드들로 오름차순 정렬해준 뒤 출력한다.
- 그렇지 않다면 이 그래프에는 k 안에 갈 수 있는 경로가 없는 것이므로 -1을 출력한다.
'개발 > Algorithm' 카테고리의 다른 글
| [프로그래머스] 위클리 챌린지 2주차(python) (0) | 2021.08.16 |
|---|---|
| [백준] 그대, 그머가 되어(python) (0) | 2021.08.13 |
| [리트코드] Network Delay Time(python) (0) | 2021.08.01 |
| [백준] 막대기(python) (0) | 2021.07.26 |
| [리트코드] Reconstruct Itinerary(python) (0) | 2021.07.25 |



