백준, 촌수계산
2644번: 촌수계산
사람들은 1, 2, 3, …, n (1 ≤ n ≤ 100)의 연속된 번호로 각각 표시된다. 입력 파일의 첫째 줄에는 전체 사람의 수 n이 주어지고, 둘째 줄에는 촌수를 계산해야 하는 서로 다른 두 사람의 번호가 주어
www.acmicpc.net
TL;DR
- 너비 우선 탐색(BFS)
- 최단경로찾기 - 다익스트라 알고리즘(Dijkstra algorithm)
문제 요약
1. 여러 사람들에 대한 부모 자식들 간의 관계가 주어졌을 때, 주어진 두 사람의 촌수를 계산하는 프로그램을 작성하라.
2. 두 사람이 친척 관계가 없는 경우는 -1을 출력해야 한다.
- 각 사람들이 노드, 노드 간의 길이는 1인 그래프의 형태를 생각할 수 있다.
- 주어진 두 사람(노드) 간의 거리를 계산하는 문제로 해석할 수 있기 때문에 너비 우선 탐색(BFS)과 다익스트라 알고리즘(Dijkstra)을 사용하면 문제를 풀 수 있다.
입출력 형태
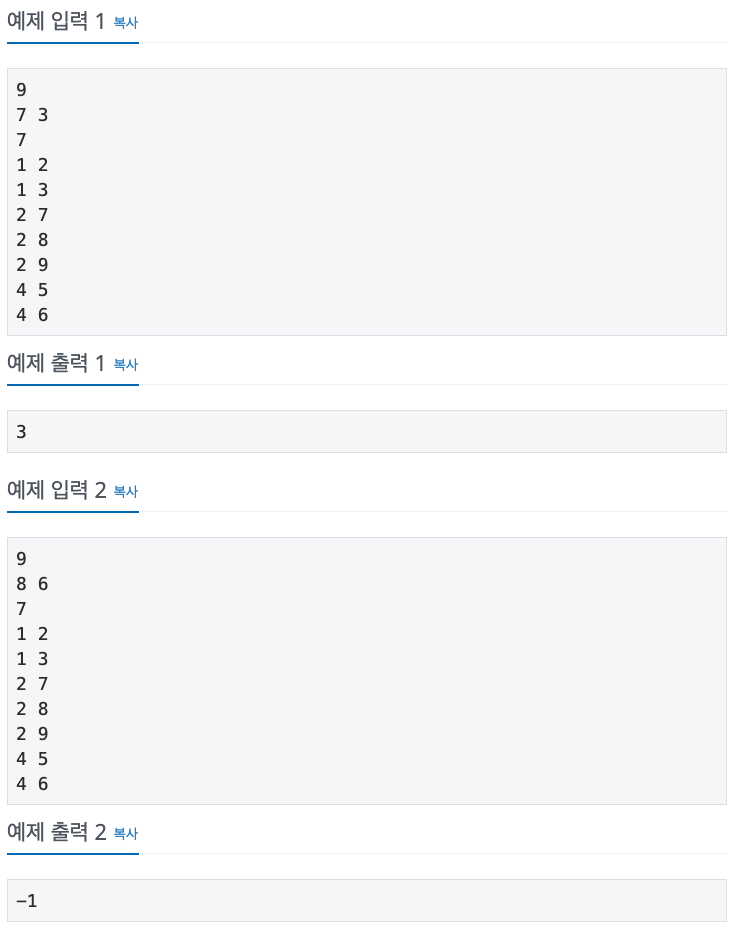
예시 2 :: 8은 1, 2, 3, 7, 9과 친척 관계이고 6은 4, 5와 친척 관계이다. 이 두 사람은 아무런 연관이 없기 때문에 -1을 출력하였다.
풀이
문제 요약에서 말한 것과 같이 가중치가 1인 그래프의 형태로 볼 수 있다. 가중치가 다를 경우에는 다익스트라 알고리즘을 사용해서 두 노드 간 거리를 구하는 방식으로 문제를 풀어야 하지만 이 문제의 경우 가중치가 1이라고 명시되어 있으므로 너비 우선 탐색으로도 문제를 해결할 수 있다.
첫 번째 방법은 너비 우선 탐색을 사용한 풀이이다.
import sys
from collections import defaultdict, deque
N = int(sys.stdin.readline())
A, B = map(int, sys.stdin.readline().split())
M = int(sys.stdin.readline())
graph = defaultdict(list)
for _ in range(M):
X, Y = map(int, sys.stdin.readline().split())
graph[X].append(Y)
graph[Y].append(X)
Q = deque([A])
visits = [0] * (N + 1)
dist = 0
while Q:
node = Q.popleft()
if node == B:
break
for v in graph[node]:
if visits[v] == 0:
visits[v] = visits[node] + 1
Q.append(v)
if visits[B] == 0:
print(-1)
else:
print(visits[B])
친척 관계를 양방향 그래프로 표현한 후 촌수를 알고 싶은 사람 중 한 명을 deque에 담는다.
- deque를 사용한 이유는 pop(0)가 O(n)의 시간복잡도인데 비해 popleft()는 O(1)의 시간복잡도를 갖기 때문이다.
visits라는 리스트를 만들어 방문한 노드(v)와 해당 노드를 방문했을 때의 거리를 갱신한다.
- visits[v]의 값이 0이라면 해당 노드는 아직 방문하지 않은 노드이므로 기존 방문한 노드인 visits[node]의 값에 1을 더한 값을 할당하여 방문한 거리와 방문했음을 표현한다.
BFS가 끝난 이후에 visits는 시작 지점(A)로부터 각 노드들을 방문한 거리가 저장되게 된다. 이 때, 우리가 원하는 사람(B)의 값이 0이라면 해당 사람과는 촌수 관계가 없는 것이므로 -1을 출력하고, 그렇지 않다면 촌수 관계가 있는 것이므로 visits[B]를 출력한다.
두 번째 방법은 다익스트라 알고리즘을 사용한 방법이다.
import sys, heapq
from collections import defaultdict
N = int(sys.stdin.readline())
X, Y = map(int, sys.stdin.readline().split())
M = int(sys.stdin.readline())
graph = defaultdict(list)
for _ in range(M):
p, c = map(int, sys.stdin.readline().split())
graph[p].append((c, 1))
graph[c].append((p, 1))
Q = [(0, X)]
dists = [-1 for _ in range(N + 1)]
while Q:
w, v = heapq.heappop(Q)
for _v, _w in graph[v]:
if dists[_v] == -1:
tmp = w + _w
dists[_v] = tmp
heapq.heappush(Q, (tmp, _v))
print(dists[Y])
앞선 방법과 차이가 있다면 노드 사이의 연결관계를 표현할 때 가중치를 함께 표현해야 한다는 것이다.(가중치를 별도로 주지 않고 너비 우선 탐색에서 사용한 방식처럼 작성해도 문제없다.)
heapq를 사용해서 거리가 짧은 노드부터 방문하며 최단 거리를 갱신한다.
이 풀이에서 dists라는 리트스틑 출발 지점인 X로부터 다른 노드들 사이의 거리를 저장하게 된다.
이처럼 그래프의 존재하는 노드 사이의 거리를 구할 때는 가중치의 값에 따라 너비 우선 탐색과 다익스트라를 선택적으로 골라서 사용할 수 있다.
'개발 > Algorithm' 카테고리의 다른 글
| [백준] 콘서트(python) (0) | 2021.10.28 |
|---|---|
| [백준] 편의점(python) (0) | 2021.10.27 |
| [백준] 연결 요소의 개수(python) (0) | 2021.10.24 |
| [리트코드] Hamming Distance(python) (0) | 2021.10.23 |
| [리트코드] Single Number(python) (0) | 2021.10.22 |



